A parallel robot is a closed-loop kinematic chain mechanism whose moving platform is
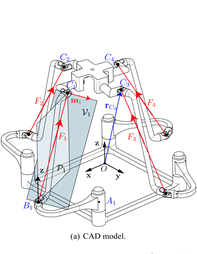
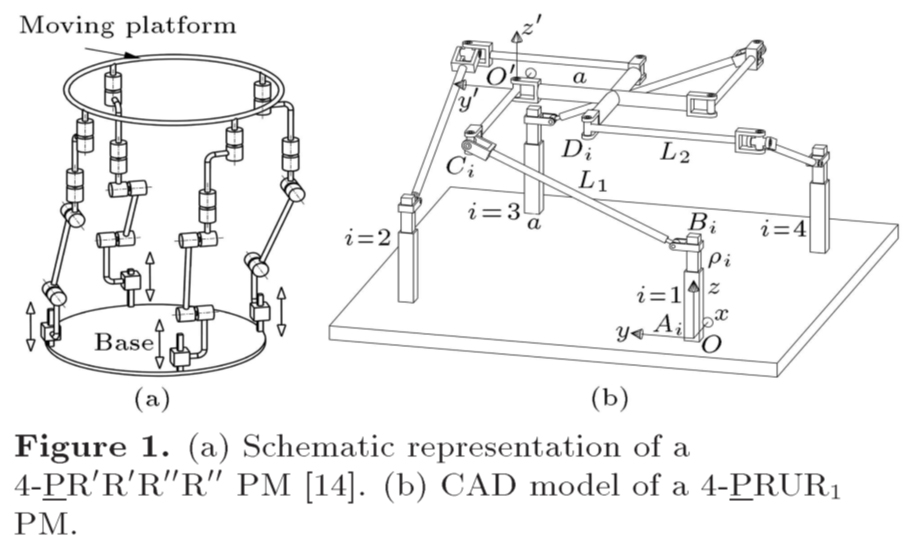
linked to the base by at least two independent kinematic chains. Due to the resulting system of nonlinear equations, the Forward Kinematic Problem (FKP) of parallel robots is complicated and cannot be easily analyzed. This thesis investigates the FKP of 4-DOF parallel robots with identical kinematic chain structures performing three translations and one rotation motion pattern, referred to as Schönflies motion. These robots have a short history and very few studies have been conducted on their kinematic characteristics. Based on the complexity of the FKP of 4-DOF parallel robots, the proposed algorithms are implemented on 3-DOF planar parallel robots, which are simpler structures, and then they are applied on 4-DOF parallel robots. First, the FKP of the parallel robots are studied in three-dimensional Euclidean space. In this approach, the joint position, kinematic constraints and resultant method are used for analysis of the FKP of parallel robots. Moreover, for the sake of comparison, the system of equations corresponding to the forward kinematic problem is solved upon resorting to Bertini software and inverse kinematic problem. Then, the FKP of parallel robots are investigated in seven-dimensional kinematic space. In this method, the FKP is analyzed by means of Denavit-Hartenberg parameters, Study’s kinematic mapping, LIA algorithm and Gröbner basis. The solutions of the FKP in sevendimensional kinematic space are mapped to the three-dimensional Euclidean space and compared to the obtained results from resultant method. More, a new algorithm is presented in sevendimensional kinematic space by means of Euler’s parameters, LIA method and interval analysis, so that this algorithm analyzes the FKP of parallel robots considering to the motion range of passive joints. The results obtained from new algorithm are compared with the results of the presented method in seven-dimensional kinematic space and fully confirmed the validity.